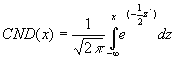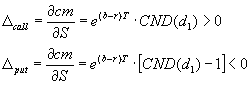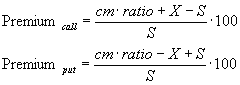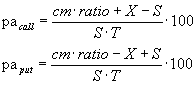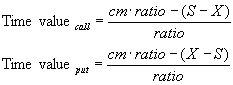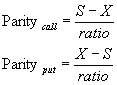Calculs d'options |
 |
Ces instruments sont basés sur des informations disponibles dans le public et ne sollicitent aucune transaction sur aucun titre représenté.
Swissquote Group Holding décline toute responsabilité concernant l'exactitude et le contenu des résultats d'analyses représentés par les indicateurs des "Warrants Full Quote"
Les informations et conclusions tirées des « Warrants Full Quote » devraient être utilisées en complément d'un jugement indépendant et impartial aux indicateurs indiqués.
Swissquote Group Holding décline toute responsabilité quant à l'exactitude, l'actualité, l'exhaustivité ou l'utilité des informations figurant dans tout le matériel disponible sur les sites de Swissquote.
Swissquote Group Holding ne souscrit à aucune opinion ou recommandation postées par les membres, ne dispense aucun conseil relatif à la fiscalité ou aux investissements, ne préconise aucun achat ou vente de titre ou d'un véhicule de placement quelconque. Nous vous recommandons la plus grande prudence face aux informations fournies, celles-ci pouvant être incomplètes et vous induire en erreur.
Avant de prendre toute décision ayant un impact financier majeur, Swissquote Group Holding vous conseille d'effectuer des investigations indépendantes et l'utilisation des informations postées se fait uniquement à vos propres risques.
Vous trouvez dans ce chapitre les Themes suivants:
|
|
Note :
Les formules et éléments intervenants dans ce document sont basés sur des options de type Européen. C'est à dire que l'exercice de l'option peut intervenir uniquement à l'échéance de l'option.
Pour vous fournir les informations suivantes nous avons du faire certaines estimations pour les calculs. Les deux seuls paramètres que nous avons estimés sont les taux d'intérêts ainsi que les dividendes futurs payés par les entreprises. Pour les Warrants étrangers nous ne tenons pas compte des dividendes distribués des titres sous-jacents.
Les données sont approximatives et peuvent différer quelque peu des données provenant d'autres sources.
La volatilité est indispensable au calcul de certains indicateurs contenus dans les données spécifiques Warrant. Il peut arriver que le calcul de la volatilité par le modèle Black Scholes ne soit pas possible. Dans ce cas, la volatilité ainsi que les indicateurs sous-jacents seront dénotés par un simple trait pour éviter tout malentendu.
Les calculs sont basés sur la quantité minimale de warrants requis pour l'exercice (Prix du warrant x Ratio).
|
Paramètres de calcul du modèle Black Scholes |
|
 |
Black & Scholes est un modèle d'évaluation développé par Fischer Black et Myron Scholes, utilisé dans la pratique par la plupart des professionnels des marchés à terme, pour calculer la prime (Prix) des options qu'ils utilisent. Ce modèle est aussi utilisé pour calculer la valeur juste ainsi que la volatilité implicite d'une option.
Les éléments qui interviennent dans les calculs :
Voici les caractéristiques essentielles de la bourse:
| S |
cours de l'actif sous-jacent |
(underlying asset price) |
| X |
prix d'exercice de l'option |
(strike price) |
| T |
durée de vie [années] |
(time to expiration) |
| r |
taux d'intérêt [%] |
(risk free interest rate) |
| b |
coût effectif [%] |
(cost of carry rate) |
| cm |
cours de l'option |
(price of option) |
 |
volatilité [%] |
(volatility) |
Autres éléments intervenant dans les calculs :
|
|
Conventions de calcul |
|
 |
Le calcul de Volatilité, Leverage, Delta, Theta, Rhô, Véga, Gamma se fait à l'aide du modèle Black-Scholes.
Ce modèle demande un certain nombre de paramètres qui peuvent être déterminés avec une part d'incertitude. Cette incertitude reflète l'écart que l'on peut trouver entre deux volatilités d'un même titre selon différentes sources d'information.
Les principaux paramètres à déterminer sont :
Le prix du sous-jacent (S)
Si le dernier trade (échange) du sous-jacent a eu lieu il y a moins d'une demi-heure:
S = underlying_asset_last
Si le dernier trade du sous-jacent a eu lieu il y a plus d'une demi-heure:
S = (underlying_asset_bid + underlying_asset_ask) / 2
Le prix de l'option (cm)
Si le dernier trade de l'option a eu lieu il y a moins d'une demi-heure:
cm = last
Si le dernier trade de l'option a eu lieu il y a plus d'une demi-heure:
cm = (bid + ask) / 2
Le taux d'intérêt (r)
On utilise les "deposit rates" de la monnaie du sous-jacent.
Ces "deposit rates" sont donnés pour différentes périodes dans le futur. On interpole linéairement entre ces points pour déterminer le r correspondant à la date d'expiration.
Les dividendes
Pour les titres suisses:
On tient compte des dividendes qui seront versés d'ici la date d'expiration de l'option pour effectuer une correction du prix du sous-jacent (DS).
On estime que si un titre a distribué un dividende il y a moins d'un an, ce même dividende sera versé dans les années qui suivent. Si par contre aucun dividende n'a été versé durant les 365 derniers jours, on estime qu'aucun dividende ne sera versé jusqu'à la date d'expiration. Si la date du versement du dernier dividende coïncide avec la date d'expiration, on n'en tient pas compte.
Correction du prix du sous-jacent :
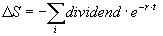
ri est le « risk free interest rate » correspondant aux dates des prochains dividendes
ti est le temps en jours jusqu'aux prochains dividendes
Pour les titres étrangers : on ne tient pas compte des dividendes.
|
Fonctions statistiques utilisées |
|
 |
|
Densité de probabilité de la loi normale réduite (Standard Normal Distribution)
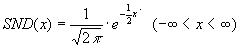 |
|
Comme pour toutes les densités de probabilité, la surface sous cette gaussienne est égale à 1 et toutes les valeurs sont positives ou nulles.
Dans ce cas la variance  2=1 et la moyenne 2=1 et la moyenne 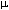 =0. =0. |
Loi normale réduite (Cumulative Normal Distribution)
Il s'agit de l'intégrale de la courbe ci-dessus.
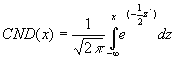
Cette intégrale ne peut être résolue analytiquement mais on peut l'approximer par :
Exemple :
Soit X une variable aléatoire suivant la loi normale réduite (gaussienne ci-dessus (variance  2=1, moyenne 2=1, moyenne 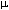 =0)), la probabilité que X soit dans un intervalle [a,b] est de : =0)), la probabilité que X soit dans un intervalle [a,b] est de :
P(a< X < b) = CND(b)-CND(a)
|
Calculs et explications |
|
 |
Vous trouvez dans ce chapitre les Themes suivants:
|
|
|
Le delta mesure la sensibilité du prix de l'option par rapport au prix du sous-jacent. Cela veut dire : de combien va varier le cours de l'option par rapport à la variation du sous-jacent.
Pour une petite variation du prix du sous-jacent on calcule la variation du prix de l'option selon :
|
|
Dans le cas d'un call 0 < delta < 1 :
| delta proche de 1 |
option "in-the-money" |
| delta = 0.5 |
option "at-the-money" |
| delta proche de 0 |
option "out-of-the-money" |
Dans le cas d'un put -1 < delta < 0 :
| delta proche de -1 |
option "in-the-money" |
| delta = -0.5 |
option "at-the-money" |
| delta proche de 0 |
option "out-of-the-money" |
Donc, le delta des Call Warrants se situe entre 0 et 1 et pour les Put Warrants entre 0 et -1.
Le delta permet également d'évaluer la probabilité que l'option arrive à l'échéance dans la monnaie (in the money) . Si delta = 0.8 alors on a 80% de chances de terminer dans la monnaie, donc avec une valeur non nulle de l'option.
Lorsque les options s'approchent de l'expiration, et sont « in the money », le delta s'approche de 1.
Un call qui est "in the money" avec un delta de 0.5 signifie un demi-point de hausse au niveau du premium pour chaque franc d'augmentation du sous-jacent. C-à-d ; si le sous-jacent augmente de 1CHF, le Warrant augmentera d'environ 0.50 CHF.
Pour un trader le Delta est le « Hedge Ratio », c.-à-d. ; s'il vend un Call qui a un delta de 0.50 il se met en position short (-1 action x delta de + 0.50 = -0.50 delta) ou simplement il est short d'une demi-action !
Calcul:
|
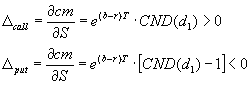 |
| S |
cours de l'actif sous-jacent |
| X |
prix d'exercice de l'option |
| T |
durée de vie [années] |
| r |
taux d'intérêt [%] |
| b |
coût effectif [%] |
| cm |
cours de l'option |
 |
volatilité [%] |
|
|
|
|
|
|
Le thêta mesure la sensibilité du prix de l'option par rapport au temps restant jusqu'à l'échéance.
Si la date d'échéance est encore lointaine, le thêta est petit. Il grandit à mesure que le date d'échéance se rapproche.
Si l'on divise le thêta par le Ratio, on obtient la variation du prix de l'option (une unité) en CHF si le lendemain le sous-jacent reste stable et clôture au même prix que la veille.
Pour une petite variation du temps jusqu'à l'expiration on calcule la variation du prix de l'option selon :
|
|
| Calcul: |
|
|
Le rhô mesure la sensibilité du prix de l'option par rapport aux variations du taux d'intérêt.
Pour une petite variation du taux d'intérêt on calcule la variation du prix de l'option selon :
|
 |
(avec r en %) |
|
|
|
|
Donc, si le taux d'intérêt augmente de 1 point de pourcentage, le prix de l'option augmente de Rhô divisé par le Ratio.
Calcul: |
|
|
Le vega mesure la sensibilité du prix de l'option par rapport à la volatilité du sous-jacent. Pour une petite variation de la volatilité du sous-jacent, on calcule la variation du prix de l'option selon :
|
 |
(avec r en %)
|
|
|
|
|
Donc, si la volatilité augmente de 1 point de pourcentage, le prix de l'option augmente de Véga divisé par le Ratio.
Calcul: |
|
|
Le gamma mesure la sensibilité du delta par rapport au prix du sous-jacent. C.-à-d., si le sous-jacent augmente de 1CHF, quel va être l'effet de cette augmentation de prix sur le delta de l'option ' Si le Gamma est grand, alors l'effet d'un point d'augmentation du sous-jacent sera important sur la valeur du delta. Il est utile de comparer différentes options sur le même sous-jacent pour avoir l'effet de levier désiré.
Logique : Si nous sommes en présence d'un Gamma élevé, la sensibilité du Delta par rapport au sous-jacent est aussi élevé, ce qui implique que le calcul du leverage sera influencé (voir le calcul du leverage).
Pour une petite variation du prix du sous-jacent on calcule la variation du delta selon :
 delta = delta =  S x gamma S x gamma
Le gamma est au maximum lorsque l'option est à la monnaie (At the Money).
Calcul:
|
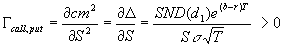 |
| S |
cours de l'actif sous-jacent |
| X |
prix d'exercice de l'option |
| T |
durée de vie [années] |
| r |
taux d'intérêt [%] |
| b |
coût effectif [%] |
| cm |
cours de l'option |
 |
volatilité [%] |
|
|
|
|
|
4.6. Volatilité |
|
 |
Il s'agit de la volatilité implicite* du sous-jacent calculée à l'aide du modèle Black Scholes. Le calcul ne tient pas compte des valeurs historiques du titre, mais uniquement des données actuelles. Ce calcul est nécessaire pour les indicateurs qui suivent.
Les paramètres de calcul sont :
- Type de l'option (call/put)
- Prix de l'option
- Ratio
- Prix du sous-jacent
- Prix d'exercice
- Temps jusqu'à l'expiration
- Taux d'intérêt
- Les dividendes attendues
* Anticipation du taux de variation sous-jacent. S'obtient en calculant la volatilité correspondant au prix actuel de l'option.
Calcul:
Méthode de Newton-Raphson (itérations):
On calcule les itérations suivantes :
|
On calcule les itérations suivantes :
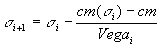 |
avec:
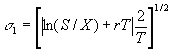
jusqu'à ce que:
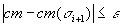 |
|
|
|
|
cm( ) est le prix de l'option calculé avec le modèle Black-Scholes selon : ) est le prix de l'option calculé avec le modèle Black-Scholes selon : |
|
4.7. Gearing |
|
 |
Le Gearing est le rapport entre le cours du sous-jacent et le cours de l'option.
Combien de fois (avec le même montant) une personne pourrait acheter, en plus, des Warrants que les actions. (Combien d'options peut-on acheter avec la contre-valeur d'une action')
Gearing = S / (cm x ratio)
S : prix du sous-jacent
cm : prix de l'option
ratio : nombre d'options nécessaire à l'exercice
Par exemple :
Cours de l'action : 500.-
Prix du Warrant : 1.-
Ratio : 25
= 500 / (25 x1) = 20
C.-à-d.; une personne peut acheter 20 fois plus de Warrants que d'actions avec la même somme d'argent pour atteindre le même gain. Plus le Gearing est grand, plus les perspectives de gain sont grandes. Attention, le risque augmente avec le gearing et vice-versa.
|
4.8. In/Out |
|
 |
Le in/out est l'écart en % entre le prix du sous-jacent et le prix d'exercice de l'option.
|
In/outcall = (S-X) / X x 100
In/output = (X-S) / X x 100
S : prix du sous-jacent
X: prix d'exercice
|
| S |
cours de l'actif sous-jacent |
| X |
prix d'exercice de l'option |
| T |
durée de vie [années] |
| r |
taux d'intérêt [%] |
| b |
coût effectif [%] |
| cm |
cours de l'option |
 |
volatilité [%] |
|
|
|
|
|
4.9. Leverage (élasticité) |
|
 |
Lvge = gearing x delta
Le leverage (élasticité) permet de mesurer le gain que l'on fait avec l'option par rapport au gain que l'on fait en achetant le sous-jacent.
Exemple: si lvge = 5, on peut gagner (ou perdre) 5 fois plus en investissant dans l'option plutôt que dans le sous-jacent pour le même montant investi.
Concrètement, si le leverage de l'option est de 5 et si le sous-jacent augmente de 4%, l'option devrait augmenter de 20%.
Le Leverage est toujours plus petit que le Gearing. Plus l'option est "out of the money" plus grande sera la différence entre les deux indicateurs.
A cause de l'effet delta, le changement du prix de l'option en Francs suisses est toujours plus petit que le changement du prix du sous-jacent. Pourtant le changement en pourcentage de l'option est plus grand que le changement en pourcentage correspondant du sous-jacent. Un changement du cours du sous-jacent de 1 % engendre un mouvement de plus de 1 % sur l'option.
|
4.10. Premium |
|
 |
Le premium est une évaluation du coût d'une option par rapport à sa valeur théorique.
|
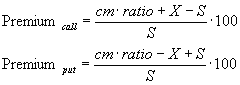 |
| S |
cours de l'actif sous-jacent |
| X |
prix d'exercice de l'option |
| T |
durée de vie [années] |
| r |
taux d'intérêt [%] |
| b |
coût effectif [%] |
| cm |
cours de l'option |
 |
volatilité [%] |
|
|
|
|
|
Bien que ce chiffre soit souvent publié et aussi discuté, il n'est pas possible de faire un jugement solide et sérieux uniquement d'après la prime. Le premium était très utilisé lorsqu'il n'existait aucun autre de modèles de calcul pour les options. Depuis 1972, ce problème est résolu et un grand choix de modèles est à disposition des investisseurs. Les investisseurs professionnels se concentrent sur une panoplie complète d'indicateurs discutés dans ce document.
Pour expliquer ce que représente ce pourcentage, prenons l'exemple suivant :
Une option avec une prime de 20% nous dit tout simplement que l'achat de l'option est 20% plus cher que l'achat du sous-jacent.
Call Warrant au prix de 0.20
Action : 250
Ratio : 25
Strike : 275
Premium = [ (0.20 x 25) + 275 - 250) / 250 ] x 100
Premium = 12 %
N'oublions pas que cette information contient la valeur temps d'une option. Aucun détail concernant cette valeur temps n'est disponible, nous ne pouvons donc pas faire de jugement dans le sens cher ou bon marché, sans avoir au moins une idée sur la valeur temps contenue dans le prix de l'option.
|
4.11. Premium annualisé |
|
 |
|
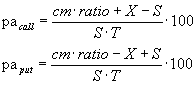 |
| S |
cours de l'actif sous-jacent |
| X |
prix d'exercice de l'option |
| T |
durée de vie [années] |
| r |
taux d'intérêt [%] |
| b |
coût effectif [%] |
| cm |
cours de l'option |
 |
volatilité [%] |
|
|
|
|
|
4.12. Time value |
|
 |
La valeur temps d'une option est la différence du prix de l'option et de la valeur intrinsèque. La valeur intrinsèque de l'option est la valeur qu'elle aurait si l'on pouvait l'exercer maintenant, soit (S-X)/ratio pour un call et (X-S)/ratio pour un put.
Si [cm x ratio-(S-X)] < 0 Time value = cm sinon:
|
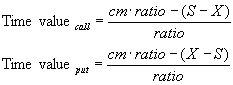 |
| S |
cours de l'actif sous-jacent |
| X |
prix d'exercice de l'option |
| T |
durée de vie [années] |
| r |
taux d'intérêt [%] |
| b |
coût effectif [%] |
| cm |
cours de l'option |
 |
volatilité [%] |
|
|
|
|
|
4.13. Parity |
|
 |
Il s'agit de la valeur intrinsèque de l'option.
|
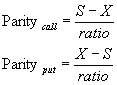 |
| S |
cours de l'actif sous-jacent |
| X |
prix d'exercice de l'option |
| T |
durée de vie [années] |
| r |
taux d'intérêt [%] |
| b |
coût effectif [%] |
| cm |
cours de l'option |
 |
volatilité [%] |
|
|
|
|
|
|