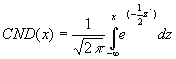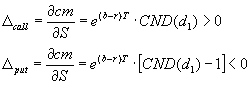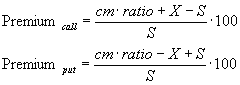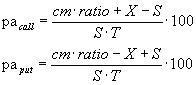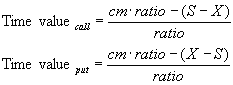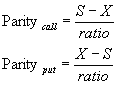Option Pricing Calculation |
 |
These instruments are based on publicly available information and do not constitute a solicitation to purchase any security represented therein.
Swissquote Group Holding declines all responsibility regarding the accuracy or contents of analysis results represented by the "Warrant Full quote" indicators.
All information and conclusions derived from "Warrant Full quote" should only be used in complement to an independent and impartial judgement on these indicators.
Swissquote Group Holding declines all responsibility regarding the accuracy, timeliness, completeness and usefulness of information available on all material provided by the Swissquote web sites.
Swissquote Group Holding does not support any opinion or recommendation posted by one of its members. Further, it does not provide any counsel regarding taxes or investments, does not recommend the purchase or sale of securities or of any investment vehicle whatsoever. We recommend that you use great caution in your perusal of the information available on this site, as such information could be incomplete or misleading.
Before reaching any decision bearing a major financial impact, Swissquote Group Holding recommends that you conduct independent investigations. Use of information posted on this site is exclusively at your own risk.
You find in this chapter the following subjects:
|
|
Note:
The formulas and elements referred to in this document apply to European-style options, i.e. options that can only be exercised on expiry.
In order to provide you with the following information, we needed to perform a number of estimations prior to calculation. The only two parameters thus estimated are interest rates and future dividends. On foreign warrants, we do not account for dividend distributions on the underlying stock.
Such indications are estimations and may differ slightly from those available from other sources.
Volatility is and indispensable parameter in the calculation of certain indicators available in the Warrants Full Quote. It may happen, however, that a specific instrument's volatility cannot be calculated by means of the Black-Scholes model. In such cases, the volatility and related indicator fields will be filled with a simple dash to avoid any misunderstanding.
Calculations are based on the minimum number of warrants required for exercise (Warrant Price x Ratio).
|
Black-Scholes Calculation Parameters |
|
 |
Black & Scholes is a pricing model developed by Fischer Black and Myron Scholes, the most commonly used by options-market professionals to calculate the premium (price) of options they are trading. This model is also applied to calculate an option's theoretical price and implied volatility.
The calculation parameters are the following:
| S |
(underlying asset price) |
| X |
(strike price) |
| T |
(time to expiration) |
| r |
(risk free interest rate) |
| b |
(cost of carry rate) |
| cm |
(price of option) |
 |
(volatility) |
Other relevant elements:
|
|
Calculation Conventions |
|
 |
Calculations of volatility, leverage, Delta, Theta, Rhô, Vega and Gamma are performed on the basis of the Black-Scholes model.
This model requires a number of parameters that can only be determined with a degree of uncertainty. This uncertainty factor explains the difference between two volatility measures of a same instrument according to two different sources of information.
The main parameters requiring determination are the following:
Underlying asset price (S)
If the underlying last traded less than half an hour ago:
S = underlying_asset_last
If the underlying last traded more than half an hour ago:
S = (underlying_asset_bid + underlying_asset_ask) / 2
Option price (cm)
If the option last traded less than half an hour ago:
cm = last
If the option last traded more than half an hour ago:
cm = (bid + ask) / 2
Rate of interest (r)
Deposit rates in the underlying asset's home currency are used.
These deposit rates are given for different points in the future. Determination of the rate of interest applicable at the option's expiry date is achieved by means of linear interpolation between these various points.
Dividends
Swiss equities:
Future dividend payments until the expiry date are taken into account to adjust the underlying asset's price (DS).
It is estimated that if a dividend was paid on a stock less than one year ago, the same dividend will be paid in future years. However, if no dividend was paid in the last 365 days, it is estimated that no dividend will be distributed before the option's expiry date. Dividend is not taken into account if the next dividend date matches the option's expiry date.
Underlying asset price correction:
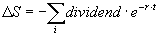
Where ri is the risk free interest rate corresponding to future dividend dates, and
ti is the time remaining, in days, until the next dividend date.
Foreign equities: Dividends are not taken into account.
|
Statistical Functions |
|
 |
|
Standard Normal Distribution
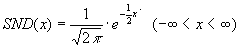 |
|
As for all probability distributions, the surface below this Gaussian curve is equal to 1 and all values are positive or equal to zero. In the present case the variance  2=1 and the mean value 2=1 and the mean value  =0. =0. |
Cumulative Normal Distribution
It is the integral of the curve displayed above.
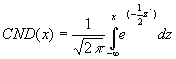
This integral cannot be analytically resolved, but can be approximated as follows:
Example:
Considering the random variable X according to the law of Standard Normal Distribution (Gaussian curve above, (variance  2=1, mean 2=1, mean  =0)), the probability that X may be found inside the interval [a,b] is the following: =0)), the probability that X may be found inside the interval [a,b] is the following:
P(a< X < b) = CND(b)-CND(a)
|
Calculations and Explanations |
|
 |
You find in this chapter the following subjects:
|
|
|
The Delta measures the option price's sensitivity to variations in the underlying asset's price. In other terms, the Delta measures by how much the option price will change in reaction to a given change in the underlying option price.
For small changes in the underlying price, the option's Delta is calculated as follows:
|
|
In the case of a call 0 £ delta £ 1:
| delta closer to 1 |
"in-the-money" option |
| delta = 0.5 |
"at-the-money" option |
| delta closer to 0 |
"out-of-the-money" option |
In the case of a put -1 £ delta £ 0:
| delta closer to -1 |
"in-the-money" option |
| delta = -0.5 |
"at-the-money" option |
| delta closer to 0 |
"out-of-the-money" option |
In other words, the Delta of a call warrant is situated between 0 and 1, and that of a put warrant between -1 and 0.
The Delta also enables an evaluation of the probability of the option being in the money when reaching its expiry date. If the Delta = 0.8, the option has an 80% chance of expiring in the money, which implies a non-zero option value.
When options near their expiry dates and are in the money, the Delta is nearing the value of 1.
An "in the money" call option with a Delta of 0.5 implies that every one-point rise in the underlying assets will result in a half-point rise in the option price: If the underlying price rises by CHF 1.00, the warrant price will increase by CHF 0.50.
For traders, the Delta is the Hedge Ratio, which means that if a trader sells a call with a Delta of 0.50, he takes on a short position: -1 share x 0.50 Delta = -0.50 Delta; in other words, he goes short by half a share.
Calculation:
|
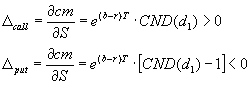 |
| S |
cours de l'actif sous-jacent |
| X |
prix d'exercice de l'option |
| T |
durée de vie [années] |
| r |
taux d'intérêt [%] |
| b |
coût effectif [%] |
| cm |
cours de l'option |
 |
volatilité [%] |
|
|
|
|
|
|
The Theta measures the option's price sensitivity to changes in the time remaining until expiry. If the expiry date is still distant, the Theta value is low. The Theta increases as the date of expiry moves closer.
If one divides the Theta by the Ratio, one obtains the option price's variation (for one unit) in CHF if, on the following day, the underlying closes at an unchanged price level.
For small time variations to expiry, the option price's variation is calculated as follows:
|
|
| Calculation: |
|
|
The Rhô measures the option price's sensitivity to changes in the rate of interest.
For small interest-rate variations, the option price's variation is calculated as follows:
|
 |
(avec r en %) |
|
|
|
|
Therefore, if the rate of risk-free interest rises by 1 percentage point, the option price rises by the value of Rhô divided by the Ratio.
Calculation: |
|
|
The Vega measures the option price's sensitivity to changes in the underlying asset's volatility. For a small change in the underlying asset's volatility, the option price's variation is calculated as follows:
|
 |
(Where r is expressed in %)
|
|
|
|
|
Therefore, if the underlying asset's volatility increases by 1 percentage point, the option price increases by the value of Vega divided by the Ratio.
Calculation: |
|
|
The Gamma measures the Delta's sensitivity to changes in the underlying asset's price. In other words, what will be the impact on the Delta if the underlying price rises by CHF 1? If the Gamma value is high, the effect of a one-point underlying price increase on the Delta will be important. It is useful to compare various options on the same underlying to find the desired leverage effect.
Logical conclusion: If we are in presence of a high Gamma, the Delta's sensitivity to the underlying price will equally be high. As a result, there will be an impact on the leverage calculation (see leverage calculation).
For a small underlying price variation, the Delta's variation is calculated as follows:
 Delta = Delta =  S x Gamma S x Gamma
The Gamma is at its maximum when the option is at the money.
Calculation:
|
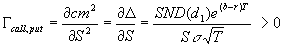 |
| S |
(underlying asset price) |
| X |
(strike price) |
| T |
(time to expiration) |
| r |
(risk free interest rate) |
| b |
(cost of carry rate) |
| cm |
(price of option) |
 |
(volatility) |
|
|
|
|
|
4.6. Volatility |
|
 |
We refer to the underlying asset's implied volatility* calculated by means of the Black-Scholes model. The calculation does not account for the underlying asset's price history, but merely for current data. This calculation is necessary in the determination of the following indicators.
Calculation parameters are the following:
- Option type (call/put)
- Option price
- Ratio
- Underlying price
- Strike price
- Time remaining to expiry
- Rate of interest
- Expected dividend payments
* Anticipation of the underlying asset's potential for price variation. The implied volatility is determined by the calculation of the volatility corresponding to the option's current price.
Calculation:
Newton-Raphson Method (iterations):
|
The following iterations are calculated:
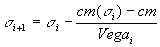 |
With:
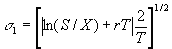
Until:
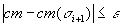 |
|
|
|
|
Where cm( ) is the option price calculated by means of the Black-Scholes method, whereby: ) is the option price calculated by means of the Black-Scholes method, whereby: |
|
4.7. Gearing |
|
 |
The gearing is the relation between the underlying asset's price and the option price.
The question is, in other terms, how many times more warrants than underlying shares could an investor buy with the same amount, or how many options can be bought with the amount required to buy one share?
Gearing = S / (cm x ratio)
S : underlying price
cm : option price
ratio : exercise ratio (number of options required to exercise into one share)
Example:
Share price: 500.-
Warrant price: 1.-
Ratio: 25
= 500 / (25 x1) = 20
In other terms, an investor must buy 20 times more warrants than shares to achieve the same gains with the same amount of money. The greater the Gearing, the higher the potential for gain. However, investors must beware of the fact that the risk increases with the Gearing value and vice versa.
|
4.8. In/Out |
|
 |
The in/out is the price differential, expressed in percentage points, between the underlying and the option.
|
n/outcall = (S-X) / X x 100
In/output = (X-S) / X x 100
S : underlying price
X: strike price
|
| S |
(underlying asset price) |
| X |
(strike price) |
| T |
(time to expiration) |
| r |
(risk free interest rate) |
| b |
(cost of carry rate) |
| cm |
(price of option) |
 |
(volatility) |
|
|
|
|
|
4.9. Leverage (elasticity) |
|
 |
Leverage = gearing x delta
The leverage (elasticity) compares gains on an option investment with gains on a purchase of the option's underlying asset.
Example: If Leverage = 5, one can gain (or lose) 5 times more by buying the option than by investing the same amount in the underlying asset.
In effect, if the option's leverage is 5 and if the underlying gains 4% in price, the option price should register a 20% increase.
The Leverage is always smaller than the Gearing. The more the option is out of the money, the greater the difference between these two indicators.
Owing to the Delta effect, the option price change (in CHF) is always less than the underlying price change. Yet the percent change in the option price is greater than that of the underlying price. A 1-% price change in the underlying generates a 1-% price movement on the option.
|
4.10. Premium |
|
 |
The Premium is an option's price valuation relative to its theoretical value.
|
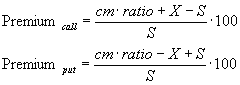 |
| S |
(underlying asset price) |
| X |
(strike price) |
| T |
(time to expiration) |
| r |
(risk free interest rate) |
| b |
(cost of carry rate) |
| cm |
(price of option) |
 |
(volatility) |
|
|
|
|
|
Although this figure is often published and discussed, it is impossible to derive a solid and serious judgement from the premium only. The Premium was largely in use at a time when no other option pricing models were available. Since 1972, this vacuum was filled by a vast number of models among which investors may now choose. Professional investors focus on a comprehensive set of all indicators discussed in this document.
To explain what this percentage rate expresses, consider the following example:
An option with a 20% premium simply expresses that buying the option is 20% more expensive than buying the underlying asset.
Call Warrant at a price of 0.20
Share: 250
Ratio: 25
Strike: 275
Premium = [ (0.20 x 25) + 275 - 250) / 250 ] x 100
Premium = 12 %
Let us not forget that this information contains an option's time value. No detail regarding this time value is available, which keeps us from making any assessments in terms of cheapness or expensiveness without at least a general idea about the time value inherent to the option price.
|
4.11. Annualised Premium |
|
 |
|
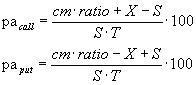 |
| S |
(underlying asset price) |
| X |
(strike price) |
| T |
(time to expiration) |
| r |
(risk free interest rate) |
| b |
(cost of carry rate) |
| cm |
(price of option) |
 |
(volatility) |
|
|
|
|
|
4.12. Time value |
|
 |
An option's time value is the differential between the option's price and its intrinsic value. The latter is defined by what the option would be worth if one could exercise it immediately, i.e. (S
If [cm x ratio-(S-X)] < 0 ® Time value = cm, otherwise:
|
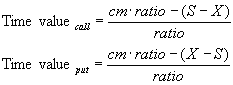 |
| S |
(underlying asset price) |
| X |
(strike price) |
| T |
(time to expiration) |
| r |
(risk free interest rate) |
| b |
(cost of carry rate) |
| cm |
(price of option) |
 |
(volatility) |
|
|
|
|
|
4.13. Parity |
|
 |
The Parity is the option's intrinsic value.
|
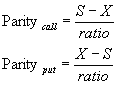 |
| S |
(underlying asset price) |
| X |
(strike price) |
| T |
(time to expiration) |
| r |
(risk free interest rate) |
| b |
(cost of carry rate) |
| cm |
(price of option) |
 |
(volatility) |
|
|
|
|
|
|