HELP > Bond |
Back | Print |
| << Back | Next >> |
| COUPON |
| The coupon is the amount the debtor undertakes to pay periodically to the investor. The coupon is a percentage of the face value of the bond. It can be paid yearly, semi-annually, quarterly or monthly. |
 |
| FREQUENCY |
|
||
The frequency indicates the interval between coupon payments. |
 |
| Italy: Two payments per year, on 01.02 and on 01.08 (2 times 2.5% of the face value) |
 |
| Belgium: One payment per year, on 28.03 (1 times 5.0% of the face value) |
| The number of coupons paid per year has an impact on the yield. According to the compound interest principle, the coupon received after six months in the context of a bond with a semi-annual coupon payment is reinvested in the market and itself yields a return. All other things being equal, the yield of a bond issue with semi-annual coupons will be higher than that of a bond issue with annual coupons. Consequently, in order to compare bonds that do not have the same coupon frequency, it is necessary to convert all yields into annualised yields: Annualised Yield = [ (1 + YTM / Freq) Freq ] - 1 YTM : Yield to maturity (yield of the issue according to its convention) Freq : Number of coupons paid over a year Example :
|
| ACCRUED DAYS |
|
||
| Number of days between the date of the last paid coupon and the value date. On 08.11.2005, you buy €100,000 of the issue below. |
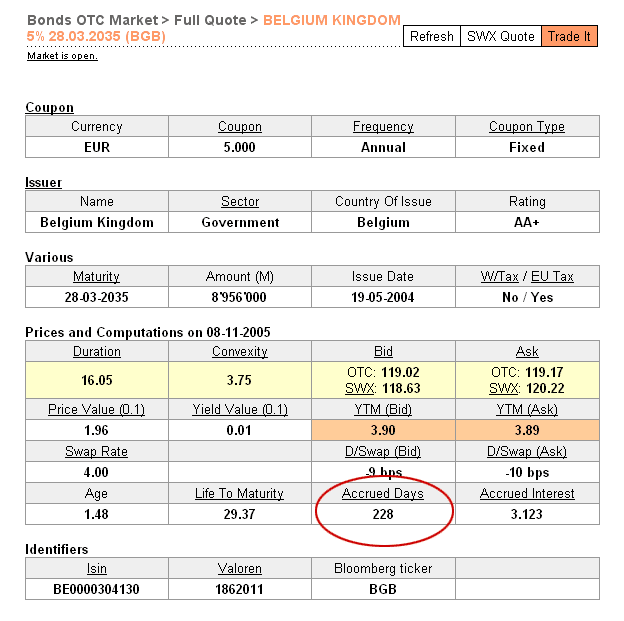 |
Date of last paid coupon: 28.03.2005 |
| ACCRUED INTEREST |
|
||
| Accrued interest represents the amount of the coupon accrued between the date of the last paid coupon and the value date. This amount is paid by the buyer and received by the seller. Although the calculation methods can vary from one country to another, the general formula is as follows: Accrued Interest = Face value x (Coupon Percentage / Frequency) x (Accrued Days / Number of Days in Period) On 08.11.2005, you buy €100,000 of the issue below. |
 |
| Date of last paid coupon: 28.03.2005 Value date (t+3): 11.11.2005 Date of next coupon payment: 28.03.2006 Accrued days: 228 (from 28.03.2005 to 11.11.2005) Number of days in the period: 365 (from 28.03.2005 to 28.03.2006) => Accrued interest: 100'000 x (0.05 / 1) x (228 / 365) = 3'123 |
| COUPON TYPE |
|
||
There are many types of coupons, the main ones being:
|
| FIXED (STRAIGHT - CLASSIC) |
|
||
| A bond that entitles payment of a fixed interest throughout the entire duration of the issue. This is the most widespread form, and these bonds are known as ‘classic’ or ‘straight’ bonds. |
| ZERO - COUPON |
|
||
| A zero-coupon is distinct from a classic bond in that no coupons are paid out. The investor’s return is based on the difference between the purchase and redemption prices. A typical example is the so-called “discount” bond. |
 |
| A zero-coupon is distinct from a classic bond in that no coupons are paid out. The investor’s return is based on the difference between the purchase and redemption prices. A typical example is the so-called “discount” bond. |
| VARIABLE |
|
||
| A variable bond pays coupon amounts that can vary over the duration of the issue. There are numerous types of variable bonds, the most frequent of which are Floating Rate Notes, Step Coupons and Step Ratings. |
| FLOATING RATE NOTE |
|
||
| The coupon of a floating rate note is set according to a benchmark. Most of these issues pay coupons on a quarterly basis and are a function of the 3-month Libor rate in their reference currency. That is, on the date of the new coupon, the investor takes the 3-month Libor rate and adds the margin set at the time of issue. Others are based on longer-term rates. Certain floating rate bonds have underlying minimum-coupon or maximum-coupon clauses to protect either the creditor or the debtor. |
 |
| Date of last coupon: 22.04.2005 3-month Libor rate as at 22.04.2005: 2.135% => New coupon starting 23.04.2005: 2.135 + 0.45 = 2.585% |
| The advantage of these bonds is that investors are protected against a rate rise, as the coupon is adjusted to the market rate. On the other hand, drawbacks include lower yields than those offered by straight bond. If the risk premium required by the market remains constant and is equal to the margin defining the coupon, at each coupon readjustment the price of the bond would be equal to 100%. In the event of deteriorated credit, the risk premium demanded by the market would increase, and consequently the new coupon would no longer make up for the risk premium, and the bond price would be lower than 100%. When the issuer's credit rating improves, the opposite occurs and the price goes above 100%. Between coupon dates, floating rate bonds behave exactly the same as straight bonds with the same life span. |
| STEP COUPON |
|
||
| A bond whose coupon will rise or decline during the life of the issue according to a schedule of repayments described in the issue prospectus. |
 |
| The coupon payment is 3.75% up to March of 2009, then 3.875% up to March of 2013, then 4.000% up to March of 2017, and so on . |
| STEP RATING |
|
||
| A step-rating bond is a bond whose coupon can be readjusted during the life of the issue according to the rating indicated by the rating agencies. A ‘step-up’ is said to take place when the coupon rises following a lowering of the bond’s rating, while a ‘step-down’ occurs when the coupon declines following an improvement in the bond’s rating. This clause reduces the volatility of the bond’s price . |
 |
| The coupon increases by 50 bps for each drop in the bond’s rating below A by S&P and Moody’s. The coupon declines by 50 bps for each increase in the bond’s rating above BBB by S&P and Moody’s On 07.11.2001, the bond issue date, the issue rating was A- and A3. In April 2002, both agencies lowered the rating of Deutsche Telekom’s bond issue to BBB+ and Baa1, respectively. Consequently, the following coupon is adjusted upward: Coupon = 6.625% + 0.500% = 7.125% If the market required BBB+/Baa1 to provide an annual yield of 7.125% in April of 2002, then with the new coupon, the bond price would be 100%. On the other hand, if the coupon remains unchanged at 6.625%, the price would be lower than 100% in order to achieve a 7.125% annual yield. |
| INFLATION LINKED |
|
||
| A bond whose face value is adjusted according to the Consumer Price Index (CPI). This adjustment is reflected as well in accrued interest, as the coupon multiplies the adjusted face value. This type of bond assures a certain degree of protection in an inflationary setting. Buying power is thus preserved. Example
|
| << Back | Next >> |
|
|||