The notion of convexity is probably the most difficult to grasp, but it is the most important concept in bond management. The ratio between the price and yield of a bond is not a declining linear ratio, but rather a convex linear ratio. Convexity measures the change in the curve’s slope as yield varies. It is the measure of the curvature of the relationship between price and yield. The convexity measure of a security, can be used to approximate the change in price that is not explained by duration.
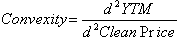
This characteristic of convexity for straight bonds has an important consequence. For an identical variation in interest rates, the price of a bond appreciates more quickly when rates are low than when they are high.
A graph might help to better understand this notion.
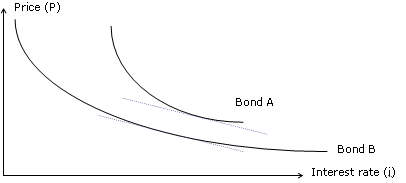
In the above graph the tangent lines have identical slopes and the two bonds have the same duration. However, notice that the estimated price change for a given variation in yield will be better for bond B than for bond A. Indeed, the function describing the price of bond B is much closer to its tangent line than the one for bond A .
The measure of convexity indicates whether duration is a good means of estimating the price change for a given variation in yield. A marked convexity means that duration is a very poor way of estimating the price change for a given variation in yield. By using duration and convexity at the same time, the best approximation of the price change for a given variation in yield is obtained :
Percentage variation in price = {[-duration x percentage variation in yield] + [convexity x (percentage variation in yield)2] } x 100
Example : What will the price of the bond shown below be if rates vary + or – 10 bps ?
|

